Datos agrupados
Cuando el tamaño de la muestra es considerable o grande y los datos numéricos son muy diversos, conviene agrupar los datos de tal manera que permita establecer patrones, tendencias o regularidades de los valores observados. De esta manera podemos condensar y ordenar los datos tabulando las frecuencias asociadas a ciertos intervalos de los valores observado.
Cuando los valores de la variable son muchos, conviene agrupar los datos en intervalos o clases para así realizar un mejor análisis e interpretación de ellos.
Los datos agrupados en frecuencia son los que se distribuyen u organizan en una tabla de frecuencia (La frecuencia es igual al número de veces en que se repite cada valor en una serie de datos.), así, Por medio de ella, es fácil identificar la cantidad de respuestas repetidas.
Los datos agrupados por intervalos son los que se organizan
dentro de un rango y se delimita su amplitud por límites establecidos. Así, por
medio de esta, es fácil identificar la cantidad de elementos en un determinado
rango de valores.
Rango: Llamamos rango al número de unidades de variación presente en los datos recopilados y se obtiene de la diferencia entre el dato mayor y el dato menor. Se representa con la letra R.
K: Número de intervalos, el cual siempre debe ser un número entero. Razón por la cual se deberá redondear el resultado al entero más cercano.
Valores
|
k
|
Menor 50
|
5 – 7
|
50 – 100
|
6 – 10
|
100 – 250
|
7 – 12
|
Más 250
|
10 - 26
|
Longitud: Es la amplitud de un intervalo es la diferencia entre el límite superior y el límite inferior. La longitud (L) de los intervalos puede calcularse mediante la expresión:
L=R/k
Intervalos de Clase: Son los intervalos en los que se agrupan y ordenan los valores observados. Cada uno de estos intervalos está delimitado (acotado) por dos valores extremos que les llamamos límites. Los intervalos de clase son conjuntos numéricos y deben ser excluyentes y exhaustivos; es decir, si un dato pertenece a un intervalo determinado, ya no podrá pertenecer a otro, esto quiere decir excluyentes y además todos y cada uno de los datos deberá estar contenido en alguno de los intervalos, esto les da el valor de exhaustivos.
El primer intervalo se construye de la siguiente manera: Habrá de iniciar con el dato menor, el cual será el extremo inferior del intervalo; el otro extremo se obtiene de la suma del dato menor y la amplitud, con este mismo valor iniciamos el segundo intervalo, del cual el segundo extremo se encuentra sumando al valor anterior la amplitud y este proceso se repite sistemáticamente hasta completar el total de intervalos.
El número de intervalos de clase depende del número de observaciones. Una mayor cantidad de datos requiere un mayor número de clases. Los intervalos de clase deben estar definidos por límites que permitan identificar plenamente si un dato pertenece a uno u otro intervalo. Estos límites son los valores extremos de cada intervalo. Límite inferior: Es el valor menor de cada intervalo, se denota por Li Límite superior: Es el número mayor de cada intervalo, se denota por Ls.
Límite inferior: Es el valor menor de cada intervalo, se denota por Li.
Límite superior: Es el número mayor de cada intervalo, se denota por Ls.
Marca de clase (xm): Se refiere al Punto Medio del intervalo y a través de él representaremos a todo el intervalo y una de las maneras de calcularla es promediando los valores límite de cada intervalo, su fórmula es:
xm= Li + Ls / 2
Ejemplos:

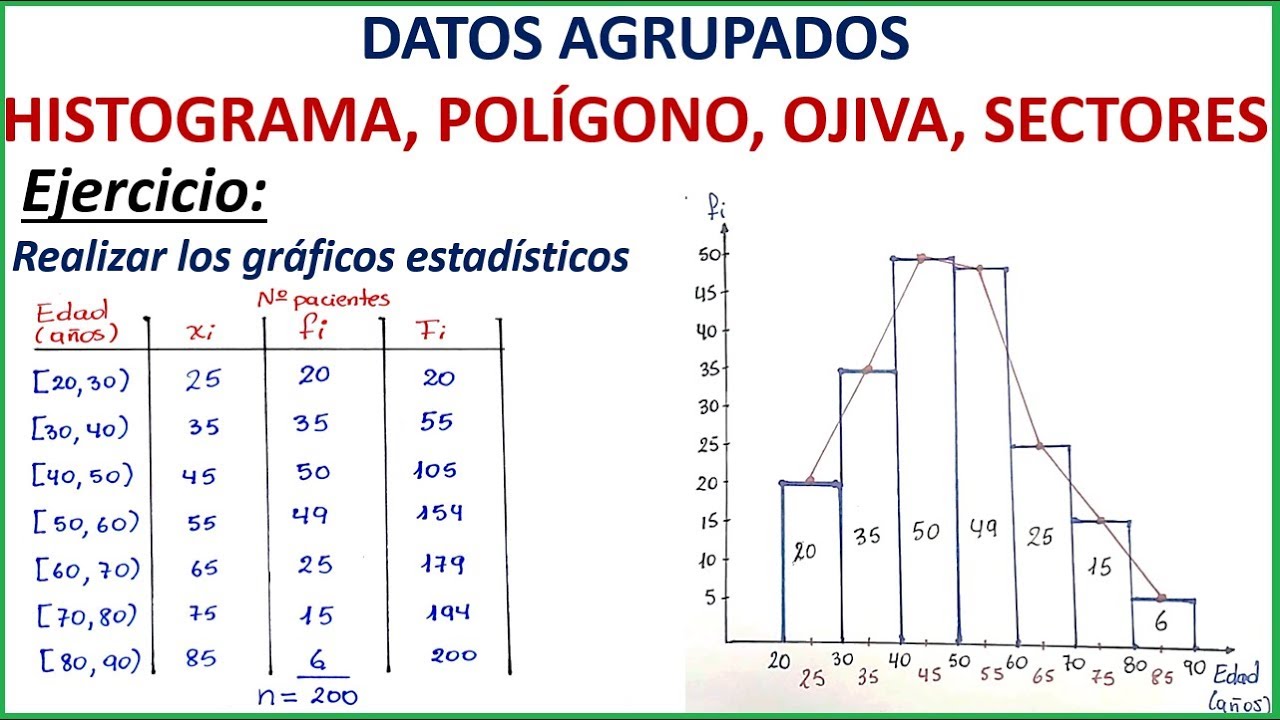
Tablas de frecuencias con datos agrupados.
ResponderEliminarCuando los valores de la variable son muchos, conviene agrupar los datos en intervalos o clases para así realizar un mejor análisis e interpretación de ellos.
• Para construir una tabla de frecuencias con datos agrupados, conociendo los intervalos, se debe determinar la frecuencia absoluta (fi) correspondiente a cada intervalo, contando la cantidad de datos cuyo valor está entre los extremos del intervalo. Luego se calculan las frecuencias relativas y acumuladas, si es pertinente.
• Si no se conocen los intervalos, se pueden determinar de la siguiente manera: (recuerda que los intervalos de clase se emplean si las variables toman un número grande de valores o la variable es continua).
- Se busca el valor máximo de la variable y el valor mínimo. Con estos datos se determina el rango.
- Se divide el rango en la cantidad de intervalos que se desea tener,(por lo general se determinan 5 intervalos de lo contrario es ideal que sea un numero impar por ejemplo 5, 7, 9) obteniéndose así la amplitud o tamaño de cada intervalo.
- Comenzando por el mínimo valor de la variable, que será el extremo inferior del primer intervalo, se suma a este valor la amplitud para obtener el extremo superior y así sucesivamente.
DATOS AGRUPADOS
ResponderEliminarLos datos agrupados son aquellos datos que pertenecen a un tamaño demuestra mayor a 30 o más elementos, por lo que para ser analizados requieren ser agrupados en clases a partir de ciertas características.Su objetivo es resumir la información
TABLA DE FRECUENCIA DE DATOS NO AGRUPADOS
Cuando la muestra consta de 30 o más datos, lo aconsejable es agrupar los datos en clases y a partir de estas determinar las características de la muestra y por consiguiente las de la población de donde fue tomada.
Una tabla de frecuencias se puede construir a partir de intervalos o clases, para ello se utiliza el número de intervalos y el tamaño del intervalo.
PASOS PARA AGRUPAR DATOS
a. Determinar el rango o recorrido de los datos.
Rango = Valor mayor – Valor menor
b. Establecer el número de clases (k)en que se van a agrupar los datos tomando como base para esto la siguiente tabla.
Tamaño de muestra o No. De datos Número de clases
Menos de 50 5 a 7
50 a 99 6 a 10
100 a 250 7 a 12
250 en adelante 10 a 20
El uso de esta tabla es uno de los criterios que se puede tomar en cuenta para establecer el número de clases en las que se van a agrupar los datos, existen otros para hacerlo.
c. Determinar la amplitud de clase para agrupar (C).
C= Rango/K
d. Formar clases y agrupar datos.
Para formar la primera clase, se pone como límite inferior de la primera clase un valor un poco menor que el dato menor encontrado en la muestra y posteriormente se suma a este valor C, obteniendo de esta manera el límite superior de la primera clase, luego se procede a obtener los límites de la clase siguiente y así sucesivamente.
Las distribuciones de frecuencias están basadas en la reducción de datos mediante la agrupación de los mismos que se presentan mediante las tablas estadísticas que son agrupaciones de datos ordenados con arreglo a un criterio lógico, procesos que se denominan tabulación.
ResponderEliminarLas tablas de frecuencia con datos agrupados es aquella distribución en la que la disposición tabular de los datos estadísticos se encuentra ordenada en clases y con la frecuencia en cada clase; es decir, los datos originales de varios valores del conjunto se combinan para formar un intervalo de clase.
La distribución de frecuencias agrupadas o tabla con datos agrupados se emplea si las variables tienden a grandes valores o la variable es continua. Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.
Tabla de datos agrupados
ResponderEliminarProcedimiento para su construcción:
1) Ordenar los datos de menor a mayor
2) Cálculo del rango: R= Dato mayor menos Dato menor
3) Designación del número de clases se puede hacer de dos maneras:
I) 1 + 3.3 Log n
Dónde:
K=Número de intervalos el cual siempre debe ser un número entero. Razón por la cual se deberá redondear el resultado al entero más cercano.
n= Número de datos
Log = logaritmo en base de 10
II) Otra regla utilizada es :la de Velleman que establece que el número de Intervalos se obtiene de la raíz cuadrada del número de datos; es decir K=?n , recomendable para tamaños de muestra pequeños (n< 50)
4) Obtención de la amplitud o anchura que tendrá cada intervalo.
Se encuentra dividiendo el rango por el número de intervalos.
Se representa con la letra A de tal manera que Ac = R/K
5) Cálculo de los límites de clase
Para construir los límites de clase ( límite inferior Li y límite superior Ls) se coloca como límite inferior de la primera clase al valor más pequeño de los datos brutos
6) Cálculo de los límites reales de clase
En seguida se calculan los límites reales de clase, llamados también fronteras de clase. Estos se calculan a partir de los límites de clase, restándole media unidad (u/2) a los límites inferiores de clase y sumándole la misma cantidad a los límites superiores. u/2 = 1/2 = 0.5
7) Conteo y Frecuencia Absoluta
El conteo es la asignación de cada dato en la clase que le corresponde. La frecuencia absoluta es el número de datos que se encuentran ubicados en cada clase.
8) Frecuencia Relativa
La frecuencia relativa es la proporción de los datos que se encuentran en cada clase. Se calcula dividiendo la frecuencia absoluta entre el total de los datos y se puede expresar como una fracción o en forma de porcentaje.
9) Frecuencias Absolutas y Relativas Acumuladas
Para agregar a la tabla de distribución de frecuencias las frecuencias acumuladas, tanto absolutas como relativas, hay que generar la columna menor que (<)
La importancia De la Tabla de Datos Agrupados
ResponderEliminarEs una manera de organizar una base de datos para tener una percepción mas clara de ellos.
A las empresas y a muchas otras organizaciones les son muy útiles para el estudio del mercado o la población cuando van a lanzar al mercado algún producto.
Uno de los componentes principales y característicos de "La Tabla de Datos Agrupados" es la MARCA DE CLASE (Xn).
ResponderEliminarLa marca de clase es el punto medio de cada intervalo,es el valor que representa a todo el intervalo para el cálculo de algunos parámetros como la media aritmética o la desviación.
ResponderEliminarLa tabla de frecuencias agrupadas se emplea generalmente si las variables toman un número grande de valores o la variable es continua.
En este caso se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.
Las clases deben ser excluyentes y exhaustivas, es decir que cada elemento de la muestra debe pertenecer a una sola clase y a su vez, todo elemento debe pertenecer a alguna clase.
Cada clase está delimitada por el límite inferior de la clase y el límite superior de la clase.
Los intervalos se forman teniendo presente que el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece intervalo, se cuenta en el siguiente intervalo. No existe una regla fija de cuantos son los intervalos que se deben hacer; hay diferentes criterios, la literatura especializada recomienda considerar entre 5 y 20 intervalos. El número de intervalos se representa por la letra "K".
Las Tablas de frecuencias son herramientas de Estadística donde se colocan los datos en columnas representando los distintos valores recogidos en la muestra y las frecuencias (las veces) en que ocurren.
ResponderEliminarLa Tabla de frecuencia de datos agrupados aquella distribución en la que los datos estadísticos se encuentran ordenados en clases y con la frecuencia de cada clase; es decir, los datos originales de varios valores adyacentes del conjunto se combinan para formar un intervalo de clase.
La tabla de frecuencias agrupadas se emplea generalmente si las variables toman un número grande de valores o la variable es continua.
TABLA DE DATOS AGRUPADOS..!
ResponderEliminarCuando los valores de la variable son muchos, conviene agrupar los datos en intervalos o clases para así realizar un mejor análisis e interpretación de ellos.
• Para construir una tabla de frecuencias con datos agrupados, conociendo los intervalos, se debe determinar la frecuencia absoluta (fi) correspondiente a cada intervalo, contando la cantidad de datos cuyo valor está entre los extremos del intervalo. Luego se calculan las frecuencias relativas y acumuladas, si es pertinente.
• Si no se conocen los intervalos, se pueden determinar de la siguiente manera: (recuerda que los intervalos de clase se emplean si las variables toman un número grande de valores o la variable es continua).
- Se busca el valor máximo de la variable y el valor mínimo. Con estos datos se determina el rango.
- Se divide el rango en la cantidad de intervalos que se desea tener,(por lo general se determinan 5 intervalos de lo contrario es ideal que sea un numero impar por ejemplo 5, 7, 9) obteniéndose así la amplitud o tamaño de cada intervalo.
- Comenzando por el mínimo valor de la variable, que será el extremo inferior del primer intervalo, se suma a este valor la amplitud para obtener el extremo superior y así sucesivamente.
• Otra forma de calcular la cantidad de intervalos es aplicando los siguientes metodos:
Método Sturges: k = 1 + 3,332 log n
donde:
k= número de clases
n= tamaño muestral
Debemos tener en cuenta 2 cosas. Primero que el número de intervalos me tiene que dar impar, segundo que el resultado se redondea generalmente a la baja. Si al redondear a la baja nos da como resultado un número par debemos redondear al alza. Este es el método que tiene mayor precisión.
Método Empírico: este método depende del criterio del evaluador de los datos, por lo tanto es arbitrario. Dice lo siguiente.
5 ≥ k ≥ 20
Veamos como se resuelve el siguiente ejercicio del libro Santillana 8:
En un centro comercial, se consultó la edad a todas las personas que entraban entre las 12:00 h y 12:30 h. Los resultados obtenidos fueron los siguientes:
tablas_de_frecuencias_datos_agrupados.jpg (416×149)
- Construye una tabla de frecuencias cuyos datos estén agrupados en ocho intervalos.
1°Para poder construir la tabla de frecuencias lo primero que debemos hacer es calcular el rango.
El rango da la idea de proximidad de los datos a la media. Se calcula restando el dato menor al dato mayor.
El dato mayor y el menor lo hemos destacado con color rojo:
Dato mayor - dato menor = 73 - 1 = 72
Por lo tanto; Rango = 72
2° En el problema nos dicen que debemos agruparlo en 8 intervalos o clases, con este dato podemos calcular la amplitud o tamaño de cada intervalo, dividiendo el valor del rango por la cantidad de intervalos que se desean obtener (en este caso son 8).
Amplitud: La amplitud de un intervalo es la diferencia entre el límite superior y el límite inferior. La amplitud(A) de los intervalos puede calcularse mediante la expresión:
tablas_de_frecuencias_datos_agrupados_amplitud.jpg (273×97)
72 / 8 = 9
Por lo tanto la amplitud de cada intervalo será de 9
- El valor de la amplitud se redondea al número inmediato superior de acuerdo a la cantidad de decimales que tienen los datos o según la precisión con que se desea trabajar.
- Puede haber intervalos con distinta amplitud.
- Puede haber intervalos con amplitud indefinida (intervalos abiertos)
marca de clase .- La marca de clase es el punto medio de cada intervalo. La marca de clase es el valor que representa a todo el intervalo para el cálculo de algunos parámetros como la media artmética o la desviación típica.
La distribución de frecuencias agrupadas o tabla con datos agrupados se emplea si las variables toman un número grande de valores o la variable es continua. Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente. Límites de la clase. Cada clase está delimitada por el límite inferior de la clase y el límite superior de la clase.
ResponderEliminarLa amplitud de la clase es la diferencia entre el límite superior e inferior de la clase. La marca de clase es el punto medio de cada intervalo y es el valor que representa a todo el intervalo para el cálculo de algunos parámetros. En caso de que el primer intervalo sea de la forma (-∞,k], o bien [k,+∞) donde k es un número cualquiera, en el caso de (-∞,k], para calcular la marca de clase se tomará la amplitud del intervalo adyacente a el (ai+1), y la marca de clase será ((k-ai+1) +k)/2. En el caso del intervalo [k,+∞) también se tomará la amplitud del intervalo adyacente a el (ai-1) siendo la marca de clase ((k+ai-1)+k)/2.
En cuanto a la función de las tablas de frecuencia agrupadas, la Estadística les confiere la de recibir los datos, agrupados en intervalos o clases, cuando los valores de una variable se caracterizan por ser muchos. En este sentido, también se identifican varias formas de construir este tipo de tablas. A continuación, algunas de ellas:
1.- La primera forma en que se puede construir una tabla de frecuencias con datos agrupados, la cual resulta también ser la más sencilla, indica que una vez la persona conoce los intervalos, debe proceder a calcular la Frecuencia Absoluta de cada uno de ellos. Así mismo, se deben calcular la Frecuencia Relativa y la Frecuencia Acumulada.
2.- No obstante, si la persona no conoce los intervalos, primero deberá enfocarse en la tarea de calcularlos, con lo cual podrá tener una idea de cuán próximos se encuentran los datos del valor tomado como media. Matemáticamente hablando, se debe restar el valor menor al mayor. El resultado es el equivalente al rango, una vez con este número, se deberá entonces agrupar los datos, según los intervalos o clases estipulados, los cuales dependerán también si son Variables Cuantitativas Discretas o por el contrario Variables Cuantitativas Continuas.
De esta forma entonces los pasos a seguir para construir una tabla de datos agrupados, será entonces los siguientes:
1.- Precisar los datos.
2.- Localizar el valor menor y el mayor.
3.- Restar estos valores, a fin de obtener el rango.
4.- Se divide esta cantidad por el número de intervalos que se busquen establecer, buscando que éste sea un número entre seis y quince.
5.- Se establecen entonces los intervalos.
Las distribuciones de frecuencias son tablas que resumen los datos originales de sus frecuencias y se emplea si las variables tienden a grandes valores o la variable es continua. Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.
ResponderEliminarExisten los tipos de frecuencia que pueden ser:
- Frecuencia Absoluta (f).- Es el número de veces que se repite el valor de cada variable. La suma de frecuencias absolutas es siempre al total de datos observados.
- Frecuencia Relativa (fr).- Indica la proporción con que se repite un valor. Es el cociente entre la frecuencia absoluta y el número total de datos. La suma de las frecuencias relativas es siempre 1
- Frecuencia Acumulada (fa).- Indica el número de valores que son menores o iguales que el valor dado. Es la suma de la frecuencia absoluta primera con la segunda, este valor con la tercera, y así sucesivamente.
- Frecuencia Porcentual (f%).- Llamada también frecuencia relativa porcentual. Se obtiene multiplicando la frecuencia relativa por 100. La suma de las frecuencias porcentuales es siempre 100%. Se calcula así:
Las distribuciones de frecuencias son tablas que resumen los datos originales de sus frecuencias y se emplea si las variables tienden a grandes valores o la variable es continua. Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.
ResponderEliminarExisten los tipos de frecuencia que pueden ser:
- Frecuencia Absoluta (f).- Es el número de veces que se repite el valor de cada variable. La suma de frecuencias absolutas es siempre al total de datos observados.
- Frecuencia Relativa (fr).- Indica la proporción con que se repite un valor. Es el cociente entre la frecuencia absoluta y el número total de datos. La suma de las frecuencias relativas es siempre 1
- Frecuencia Acumulada (fa).- Indica el número de valores que son menores o iguales que el valor dado. Es la suma de la frecuencia absoluta primera con la segunda, este valor con la tercera, y así sucesivamente.
- Frecuencia Porcentual (f%).- Llamada también frecuencia relativa porcentual. Se obtiene multiplicando la frecuencia relativa por 100. La suma de las frecuencias porcentuales es siempre 100%. Se calcula así:
Las distribuciones de frecuencias son tablas que resumen los datos originales de sus frecuencias y se emplea si las variables tienden a grandes valores o la variable es continua. Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente.
ResponderEliminarExisten los tipos de frecuencia que pueden ser:
- Frecuencia Absoluta (f).- Es el número de veces que se repite el valor de cada variable. La suma de frecuencias absolutas es siempre al total de datos observados.
- Frecuencia Relativa (fr).- Indica la proporción con que se repite un valor. Es el cociente entre la frecuencia absoluta y el número total de datos. La suma de las frecuencias relativas es siempre 1
- Frecuencia Acumulada (fa).- Indica el número de valores que son menores o iguales que el valor dado. Es la suma de la frecuencia absoluta primera con la segunda, este valor con la tercera, y así sucesivamente.
- Frecuencia Porcentual (f%).- Llamada también frecuencia relativa porcentual. Se obtiene multiplicando la frecuencia relativa por 100. La suma de las frecuencias porcentuales es siempre 100%. Se calcula así:
Para construir una tabla de frecuencias con datos agrupados, conociendo los intervalos, se debe determinar la frecuencia absoluta (fi) correspondiente a cada intervalo, contando la cantidad de datos cuyo valor está entre los extremos del intervalo. Luego se calculan las frecuencias relativas y acumuladas, si es pertinente.
ResponderEliminar• Si no se conocen los intervalos, se pueden determinar de la siguiente manera: (recuerda que los intervalos de clase se emplean si las variables toman un número grande de valores o la variable es continua).
- Se busca el valor máximo de la variable y el valor mínimo. Con estos datos se determina el rango.
- Se divide el rango en la cantidad de intervalos que se desea tener,(por lo general se determinan 5 intervalos de lo contrario es ideal que sea un numero impar por ejemplo 5, 7, 9) obteniéndose así la amplitud o tamaño de cada intervalo.
- Comenzando por el mínimo valor de la variable, que será el extremo inferior del primer intervalo, se suma a este valor la amplitud para obtener el extremo superior y así sucesivamente.
Cuando la muestra consta de 30 o más datos, lo aconsejable es agrupar los datos en clases y a partir de estas determinar las características de la muestra y por consiguiente las de la población de donde fue tomada.
ResponderEliminarAntes de pasar a definir cuál es la manera de determinar las características de interés (media, mediana, moda, etc.) cuando se han agrupado en clases los datos de la muestra, es necesario que sepamos como se agrupan los datos.
Cuando la muestra consta de 30 o más datos, lo aconsejable es agrupar los datos en clases y a partir de estas determinar las características de la muestra y por consiguiente las de la población de donde fue tomada.
Antes de pasar a definir cuál es la manera de determinar las características de interés (media, mediana, moda, etc.) cuando se han agrupado en clases los datos de la muestra, es necesario que sepamos como se agrupan los datos.
Una tabla de frecuencias se puede construir a partir de intervalos o clases, para ello se utiliza el número de intervalos y el tamaño del intervalo.
Números de Intervalos: El número de intervalos es la cantidad de veces que se debe de realizar las iteraciones, es decir la cantidad de filas que se deben de realizar en la tabla. Se puede calcular de la siguiente manera:
Calculando la raíz cuadrada de n, donde ésta es la cantidad de datos de la encuesta.
√n
Tamaño del intervalo: El tamaño del intervalo es el rango que existe entre dos números, en donde para formar la primera clase, se pone como límite inferior de la primera clase un valor un poco menor que el dato menor encontrado en la muestra y posteriormente se suma a este valor el tamaño del intervalo, obteniendo de esta manera el límite superior de la primera clase, luego se procede a obtener los límites de la clase siguiente y así sucesivamente.
Cuando los valores de la variable son muchos, conviene agrupar los datos en intervalos o clases para así realizar un mejor análisis e interpretación de ellos.
• Para construir una tabla de frecuencias con datos agrupados, conociendo los intervalos, se debe determinar la frecuencia absoluta (fi) correspondiente a cada intervalo, contando la cantidad de datos cuyo valor está entre los extremos del intervalo. Luego se calculan las frecuencias relativas y acumuladas, si es pertinente.
• Si no se conocen los intervalos, se pueden determinar de la siguiente manera: (recuerda que los intervalos de clase se emplean si las variables toman un número grande de valores o la variable es continua).
- Se busca el valor máximo de la variable y el valor mínimo. Con estos datos se determina el rango.
- Se divide el rango en la cantidad de intervalos que se desea tener,(por lo general se determinan 5 intervalos de lo contrario es ideal que sea un numero impar por ejemplo 5, 7, 9) obteniéndose así la amplitud o tamaño de cada intervalo.
- Comenzando por el mínimo valor de la variable, que será el extremo inferior del primer intervalo, se suma a este valor la amplitud para obtener el extremo superior y así sucesivamente.
• Otra forma de calcular la cantidad de intervalos es aplicando los siguientes metodos:
Método Sturges: k = 1 + 3,332 log n
donde:
k= número de clases
n= tamaño muestral
Debemos tener en cuenta 2 cosas. Primero que el número de intervalos me tiene que dar impar, segundo que el resultado se redondea generalmente a la baja. Si al redondear a la baja nos da como resultado un número par debemos redondear al alza. Este es el método que tiene mayor precisión.
Método Empírico: este método depende del criterio del evaluador de los datos, por lo tanto es arbitrario. Dice lo siguiente.
5 ≥ k ≥ 20
TABLA DE DATOS AGRUPADOS
ResponderEliminarCuando los valores de la variable son muchos, conviene agrupar los datos en intervalos o clases para así realizar un mejor análisis e interpretación de ellos.
• Para construir una tabla de frecuencias con datos agrupados, conociendo los intervalos, se debe determinar la frecuencia absoluta (fi) correspondiente a cada intervalo, contando la cantidad de datos cuyo valor está entre los extremos del intervalo. Luego se calculan las frecuencias relativas y acumuladas, si es pertinente.
• Si no se conocen los intervalos, se pueden determinar de la siguiente manera: (recuerda que los intervalos de clase se emplean si las variables toman un número grande de valores o la variable es continua).
- Se busca el valor máximo de la variable y el valor mínimo. Con estos datos se determina el rango.
- Se divide el rango en la cantidad de intervalos que se desea tener,(por lo general se determinan 5 intervalos de lo contrario es ideal que sea un numero impar por ejemplo 5, 7, 9) obteniéndose así la amplitud o tamaño de cada intervalo.
- Comenzando por el mínimo valor de la variable, que será el extremo inferior del primer intervalo, se suma a este valor la amplitud para obtener el extremo superior y así sucesivamente.
DATOS AGRUPADOS
ResponderEliminar1.- su fin es resumir la información.
2.- generalmente, los elementos son de mayor tamaño, por lo cual requieren ser agrupados, esto implica: ordenar, clasificar y expresar los en una tabla de frecuencias.
3.- se agrupa a los datos, si se cuenta con 20 o más elementos. Aunque contemos con más de 20 elementos, debe de verificarse que los datos n sean significativos, Esto es: que la información sea “repetitiva”, también debemos de verificar que los datos puedan clasificarse. Y que dicha clasificación tiene coherencia y lógica (de acuerdo a lo que se nos esta pidiendo) .
Una vez que ya hemos ordenado y clasificado, presentaremos la información obtenida mediante una ”tabla de frecuencias ”